Education

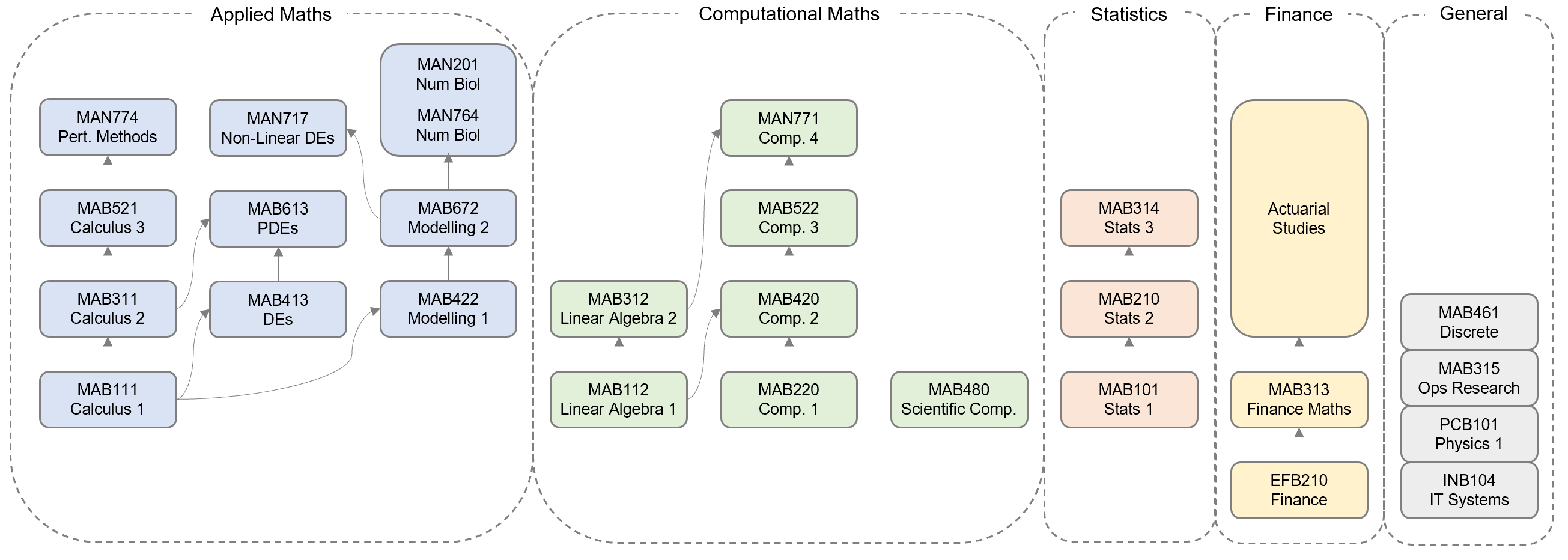
Actuarial Science    |    Statistics    |    Computational Mathematics    |    Applied Mathematics    |    General Mathematics    |    Schematic

Actuarial Science

CT1 Financial Mathematics

1. Cashflow models
2. Time value of money
3. Interest rates
4. Real and money interest rates
5. Discounting and accumulating
6. Level annuities
7. Deferred and increasing annuities
8. Equations of value
9. Loan schedules
10. Project appraisal
11. Investments
12. Elementary compound interest problems
13. Arbitrage and forward contracts
14. Term structure of interest rates
15. Stochastic interest rate models

CT2 Finance and Financial Reporting

1. Key principles of finance
2. Company ownership
3. Taxation
4. Financial instruments
5. Use of derivatives
6. Issues of shares
7. Introduction to accounts
8. The main accounts
9. Depreciation and reserves
10. Generating accounts
11. Group accounts and insurance company accounts
12. Interpretation of accounts
13. Limitation of accounts
14. Financial institutions
15. Weighted average cost of capital
16. Capital structure and dividend policy
17. Capital project appraisal

CT4 Models

1. Principles of actuarial modelling
2. Stochastic processes
3. Markov chains
4. Two-state Markov model
5. Time-homogeneous Markov jump processes
6. Time-inhomogeneous Markov jump processes
7. Survival models
8. Estimating the lifetime distribution function
9. Cox regression model
10. Binomial and Poisson models
11. Exposed to risk
12. Graduation and statistical tests
13. Methods of graduation

CT5 Contingencies

1. Life assurance contracts
2. Life annuity contracts
3. The life table
4. Evaluation of assurances and annuities
5. Net premiums and reserves
6. Variable benefits and with-profit policies
7. Gross premium and reserves
8. Annuities and assurances with two lives
9. Contingent and reversionary benefits
10. Profit testing
11. Determining reserves using profit testing
12. Competing risks
13. Multiple decrement tables
14. Pension funds
15. Mortality, selection, and standardisation

CT6 Statistical Methods

1. Decision theory
2. Bayesian statistics
3. Loss distributions
4. Reinsurance
5. Credibility theory
6. Empirical Bayes credibility theory
7. Risk models
8. Ruin theory
9. Generalised linear models
10. Run-off triangles
11. Time series

CT7 Business Economics

1. Economic concepts
2. Demand and supply
3. Elasticity and uncertainty
4. Consumer demand and uncertainty
5. Production and costs
6. Revenue and profit
7. Perfect competition and monopoly
8. Imperfect competition
9. Products, marketing and advertising
10. Growth strategy
11. Pricing strategies
12. Government intervention in markets
13. Government and the firm
14. Supply-side policy
15. International trade
16. Balance of payments and exchange rates
17. The macroeconomic environment
18. Money and interest rates
19. Business activity, unemployment and inflation
20. Demand-side macroeconomic policy

CT8 Financial Economics

1. Efficient markets hypothesis
2. Utility theory and stochastic dominance
3. Measures of investment risk
4. Portfolio theory
5. Models of asset returns
6. Asset pricing models
7. Brownian motion and martingales
8. Stochastic calculus and Itô processes
9. Stochastic models of security prices
10. Introduction to the valuation of derivative securities
11. The Greeks
12. The binomial model
13. The Black-Scholes option pricing formula
14. The 5-step method in discrete time
15. The 5-step method in continuous time
16. The term structure of interest rates
17. Credit risk

ACST831 Actuarial Control Cycle 1

1. Overview of control cycle
2. Enterprise risk management
3. Context of actuarial work
4. Assets
5. Product design
6. Modelling
7. The need for capital
8. Pricing
9. Regulation
10. Meeting consumers’ needs

ACST832 Actuarial Control Cycle 2

1. Valuing liabilities
2. Profit
3. Monitoring experience
4. Solvency
5. Regal & Occidental case study
6. Responding to experience
7. Applying risk management
8. Professionalism

ACST871 Investment management

1. Elements of investing
2. Investment theory
3. Debt securities
4. Equity and property
5. Derivatives
6. Investment management
7. Alternatives and hedge funds
8. Asset liability modelling
9. Wealth management
10. Setting investment strategy
11. Implementing investment strategy
12. Investment governance
13. Roles of actuaries

Statistics

MAB101 Statistical Data Analysis 1

1. Collecting, analysing and presenting data
2. Data features, summary statistics, estimation and parameters
3. Categorical data and proportions: Estimating proportions; testing sets of proportions; testing independence of categorical variables
4. Introduction to the analysis of continuous data: Continuous data; revision of normal distribution; interval estimates of a proportion
5. Analysis of variance (ANOVA): investigating if and how a continuous variable is affected by categorical variables
6. Regression analysis: investigating relationships between categorical variables
7. Interval estimation: behaviour of sample mean; confidence intervals for means and mean differences; tolerance intervals; prediction intervals
8. Hypothesis testing: testing hypotheses about means, proportions and variances in one or two samples

MAB210 Statistical Modelling 1

1. Events and probability; modelling and assigning probabilities in simple situations
2. Independence and conditional probability
3. Problem-solving using independence and conditional probability
4. Introduction to Markov chains
5. Random variables and distributions
6. Special discrete distributions: binomial, geometric, negative binomial, Poisson
7. Special continuous distributions: uniform, exponential, normal; Central Limit Theorem
8. Goodness-of-fit
9. Introduction to queues
10. Introduction to dependent and independent random variables

MAB314 Statistical Modelling 2

1. Markov chains
2. Simple random walk
3. Generating functions
4. Branching processes
5. Introduction to Markov processes (continuous time); birth and death processes; queues
6. Transformations of random variables
7. Special distribution results from the use of moment generating functions and transformations
8. Use of probability transformation; order statistics; approximations to moments

Computational Mathematics

MAB112 Linear Algebra

MAB312 Linear Algebra

1. Systems of linear equations and matrix algebra
2. Vector spaces
3. Inner product spaces

MAB220 Computational Mathematics 1

1. Errors; floating point arithmetic; nested multiplication
2. Roots of nonlinear functions
3. Solutions of linear systems
4. Interpolation
5. Differentiation and integration
6. Ordinary differential equations

MAB420 Computational Mathematics 2

1. Direct methods for linear systems
2. Data structures and algorithms for structured linear systems
3. Norms
4. Iterative methods for linear systems
5. Iterative methods for the eigenvalue problem

MAB480 Introduction to Scientific Computation

1. Designing a web search engine
2. Fractals: visualising the Mandelbrot set
3. Curve fitting
4. LaTeX for mathematics documentation
5. Stochastic simulation of an epidemic
6. Genetic resistance
7. A GUI for random sampling
8. Valuing share options
9. Modelling extinction risk of mallee fowl

MAB522 Computational Mathematics 3

1. Introduction to computational fluid dynamics
2. The finite volume method
3. Nonlinear systems

MAN771 Computational Mathematics 4

1. An introduction to Krylov subspace methods
2. Newton methods
3. Finite Volume Model for advection-diffusion equations
4. Extension of FVM to two dimensions; arbitrary grids; treatment of nonlinearity
5. Unconstrained optimisation
6. Constrained optimisation

Applied Mathematics

MAB111 Calculus and Differential Equations

MAB311 Advanced Calculus

1. Functions of several variables: Graphical representations
2. Functions of several variables: Limits and continuity
3. Partial derivatives
4. Linearisation, differentiability and differentials
5. Gradients and directional derivatives
6. Implicit differentiation and Taylor series approximations
7. Extreme values for functions of several variables
8. Double integrals
9. Triple integrals
10. Fourier series

MAB521 Applied Maths 3

1. Vector calculus
2. Partial differential equations of applied mathematics
3. The heat equation
4. The wave equation
5. Laurent series

MAB413 Differential Equations

1. Posedness
2. First-order techniques
3. Exact equations
4. Solving homogeneous DEs
5. Variation of parameters
6. Cauchy-Euler equations
7. Series solutions
8. Laplace transforms
9. Systems of linear differential equations

MAB422 Mathematical Modelling

1. Introduction to mathematical modelling
2. Modelling a school influenza epidemic
3. Analysis of the SIR model
4. Predator-prey and competing species
5. Null-cline and phase plane analysis
6. Heating and cooling problems
7. Heat loss through a wall
8. Cooling a computer chip
9. Insulating a water pipe
10. Spontaneous combustion
11. Measles vaccination in NZ
12. Compartment models
13. Models of populations of species with separate generations

MAB613 Partial Differential Equations

1. Derivation of partial differential equations of mathematical physics
2. Fourier series
3. Separation of variables
4. Sturm-Liouville systems
5. Solution of homogeneous problems by separation of variables
6. Finite Fourier transforms and nonhomogeneous problems
7. Moving-boundary problems

MAB672 Advanced Mathematical Modelling

1. Introduction to ODE modelling
2. Nonlinear ODE analysis
3. Limit cycles and bifurcations
4. Introduction to modelling with PDEs
5. Travelling waves and PDEs
6. Analytic solutions of PDEs
7. Introduction to cellular automata

MAN774 Perturbation Methods

1. Introduction to perturbation expansions
2. Asymptotics
3. Strained coordinates
4. Practical applications

MAN201 Stochastic Modelling and Simulation for the Life Sciences

1. Law of Mass Action
2. Transporters and pumps
3. Model simplification
4. Continuous-time Markov chains
5. Stochastic chemistry
6. Stochastic differential equations
7. Spatial modelling
8. Towards multiscale simulation

MAN764 Numerical Biology

1. Case study: Lemmings
2. Case study: Nerve impulses
3. Case study: Cells

MAN717 Non-Linear Differential Equations

1. First-order non-linear differential equations
2. Singularity theory with a distinguished parameter
3. Second-order differential equations: steady-state solutions and their stability
4. Second-order differential equations: the absence of periodic solutions
5. Second-order differential equations: two simple applications
6. Second-order differential equations: periodic behaviour
7. Degenerate Hopf bifurcations

General Mathematics

MAB315 Operations Research 2

1. Transportation problems
2. Linear programming problems
3. Simplex method
4. Big M method
5. Sensitivity analysis
6. Duality in linear programming
7. Project scheduling: CPM and Gantt charts
8. Project scheduling: PERT

MAB461 Discrete Mathematics

1. Counting techniques
2. Basic set theory
3. Properties of the integers
4. Relations and functions
5. The principle of inclusion-exclusion
6. Generating functions
7. Relations revisited
8. Rings and modular arithmetic
9. Polynomial rings and fields

EFB210 Finance 1

1. Introduction to debt and equity
2. Financial mathematics
3. Valuation and security analysis
4. Investments as random variables
5. The two-period perfect certainty model
6. Introduction to capital budgeting
7. Introduction to portfolio theory and CAPM
8. Weighted average cost of capital
9. Efficient markets hypothesis
10. Derivatives

MAB313 Mathematics of Finance

1. Interest rates
2. Equations of value
3. Amortisation schedules
4. Annuities
5. The money market
6. The bond or fixed interest market

INB104 Building IT Systems

1. Introduction to Python
2. Life cycle of a system; algorithms and stepwise refinement; functions; parameters
3. Boolean-valued expressions; Boolean operators; conditional statement
4. Iteration
5. Recursion
6. Database concepts
7. SQL
8. Networks, the internet, web servers, protocols, HTML, file input/output
9. Functional decomposition
10. Abstract types and objects

PCB101 Foundations of Physics

Schematic